Authors & affiliations
Sarthak Saluja and Javiera Cartagena-Farias
Care Policy and Evaluation Centre, London School of Economics and Political Science
Introduction
Difference-in-differences (DiD) is a quasi-experimental method used to estimate the effect of an intervention (the treatment), usually a policy, by analysing change in outcome across a defined period-of-time (Angrist & Krueger, 1999). It is quasi-experimental, in the sense that the randomisation of units of analysis – which is otherwise considered as a gold standard for estimating causal effects – is not achievable.
The DiD approach involves the measurement of the change in outcome between two time periods (pre and post intervention) and comparing its size to the changes experienced by a credible counterfactual (or comparison group). This is to establish what would have happened to the treated group if the policy or intervention was never implemented.
For this, we must be willing to assume that the treatment group would have observed a trend like the comparison group in the absence of the policy or intervention. This assumption, known as Parallel Trends, is a difficult to test assumption. Nevertheless, knowing historical patterns can help to build a convincing argument in support of this assumption.
When to use it
Type of data needed
To conduct a DiD analysis, we need to have an appropriate and clearly defined treatment and comparison group (y_treated and y_comparison). We also need information on outcomes before and after the treatment for both the groups, that is: y_pre-treated, y_post_treated, y_pre_comparison and y_post_comparison. The analysis can be either at two points (before/after treatment) or across multiple time points. We should also have data on the baseline characteristics on the treatment and comparison groups. If the two groups differ on baseline characteristics, it is worth investigating why those differences occur, and if the causes of those differences will continue to impact the trends observed in the two groups.
Description
Method
Let us assume the two-time period scenario, where we have data on an outcome before and after the intervention. This scenario can be represented in a tabular form, as shown in Table 1.
Table 1: Example
| Pre – Treatment | Post – Treatment | Differences | |
| Treatment | 75 | 85 | 10 |
| Control | 80 | 85 | 5 |
| Differences | -5 | 0 | 5 |
The DiD calculation in this scenario is straightforward. We simply need to take the difference between the pre and post outcomes for both groups. If the parallel trends assumption holds, then the difference between the two is the required estimate for the treatment effect. This effect is formally called the Average Treatment Effect on the Treated (ATT). The same scenario can also be represented via a graph, as shown in Figure 1.
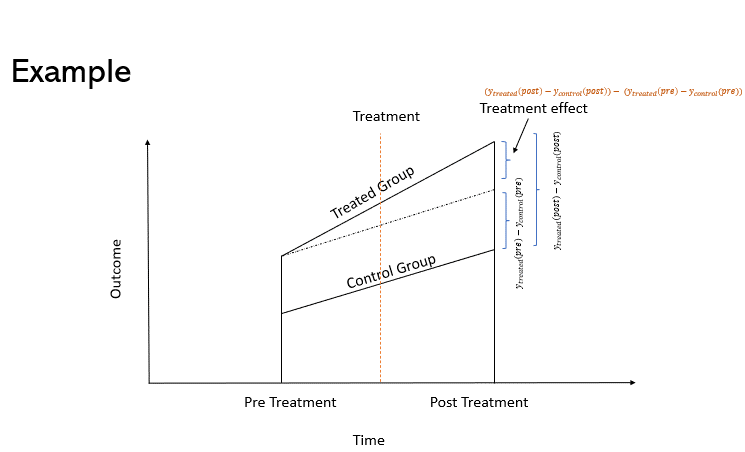
Assuming that the outcome of interest is , then the mathematical formula for ATT is given by equation 1.
Equation 1: [math]ATT=(y_{treated}^{post}-y_{control}^{post})-\ (y_{treated}^{pre}-y_{control}^{pre})[/math]
It is easy to see that Equation 1 is equivalent to calculating the difference of the differences in the groups’ outcomes post and pre-treatment. This can also be represented via a regression equation:
Equation 2: [math]y_{it}\ =\alpha_0+\alpha_1{Post}_t+\alpha_2{Treated}_i+\alpha_3({Treated}_i\ast{Post}_t)+\beta x_i+\varepsilon_{it}[/math]
In Equation 2., i represents the individual unit, t represents the time of observation, Post is a dummy variable equal to 1 if the observation is recorded after the treatment, and 0 otherwise. Treated is also a dummy variable equal to 1 if the unit received treatment and zero otherwise. In this equation, (the coefficient of interaction between Treated and Post dummy) is the ATT, as shown in Table 2.
Table 2: DiD coefficients
| Pre-Treatment
(Post = 0) |
Post -Treatment
(Post = 1) |
Difference | |
| Treatment Group (Treated = 1) | [math]\alpha_0 + \alpha_2[/math] | [math]\alpha_0 + \alpha_1 + \alpha_2 + \alpha_3[/math] | [math]\alpha_1 + \alpha_3[/math] |
| Comparison group (Treated = 0) | [math]\alpha_0 [/math] | [math]\alpha_0 + \alpha_1[/math] | [math]\alpha_1[/math] |
| Difference | [math]\alpha_2[/math] | [math]\alpha_2 + \alpha_3[/math] | [math]\alpha_3[/math] |
Parallel Trends Assumption
While it is hard to guarantee parallel trends, having data across multiple timepoints can help with establishing a case for it. Visual inspection of the trends in the groups, alongside their baseline values, can be useful. To empirically check for significant differences in the trends, another approach can be to include interactions between time variables (with the time unit right before treatment being the baseline) and treatment dummy.
In the pre-treatment period, this will tell us whether there are significant differences in the difference in outcome between the groups across the current and baseline periods. The presence of significant differences indicates the violation of parallel trends, as an external force is driving the effect in the absence of treatment. In short, there should be no treatment effect when treatment has not yet been given. In the post treatment period, this model can indicate how the treatment effect changes with time.
Example (in long-term care)
DiD is a well-established technique which has been used in many disciplines, including economics and social sciences. Many applications have been focused on evaluating the impact of educational programs, or health-related initiatives. More recently, this approach has been implemented to study causal effects on the long-term care sphere. Below, we give some examples:
- Morciano et al. (2020) explored the impact of Vanguard programs in England using a DiD approach.
- Werner, Konetzka, & Polsky (2013) estimate the effect of pay for performance scheme in US on quality of care in nursing homes, and
- Shin (2022) compared long-term care facilities against nursing hospitals among the elderly in South Korea.
Discussion
Beyond DiD
The original DiD technique has more recently been modified to include more complex evaluative designs or different data structures. For instance:
- DiD with multiple time periods (Callaway, and Sant’Anna, 2021)
- DiD with continuous treatment (Callaway, Goodman-Bacon & Sant’Anna, 2024)
- DiD in combination with Propensity score matching (Stuart et al, 2014)
- Semiparametric DiD estimators (Abadie, 2005)
- Unpooled-DiD (Karim et al., 2023)
References
Abadie, A. (2005). Semiparametric Difference-in-Differences Estimators. The Review of Economic Studies, 72(1), 1–19. http://www.jstor.org/stable/3700681
Angrist, J. & Krueger, A. (1999). Empirical strategies in labor economics. Handbook of Labor Economics, in: O. Ashenfelter & D. Card (ed.), Handbook of Labor Economics, edition 1, volume 3, chapter 23, pp. 1277-1366, Elsevier.
Callaway, B. and Sant’Anna, P (2021) Difference-in-Differences with multiple time periods, Journal of Econometrics, 225(2) pp. 200-230. https://doi.org/10.1016/j.jeconom.2020.12.001.
Callaway, B., Goodman-Bacon, A. & Sant’Anna, P. (2024) Difference-in-differences with a Continuous Treatment. National Bureau of Economic Research. Working Paper 32117. Available online here
Karim, S. Webb, M., Austin, N., and Strumpf, E. (2023). Difference-in-Differences with unpoolable data. Available online at https://www.stata.com/meeting/canada23/slides/Canada23_Karim.pdf
Morciano, M., Checkland, K., Billings, J., Coleman, A., Stokes, J., Tallack, C., & Sutton, M. (2020). New integrated care models in England associated with small reduction in hospital admissions in longer-term: A difference-in-differences analysis. Health policy (Amsterdam, Netherlands), 124(8), 826–833. https://doi.org/10.1016/j.healthpol.2020.06.004
Shin H. (2022). Comparison between the Aged Care Facilities Provided by the Long-Term Care Insurance (LTCI) and the Nursing Hospitals of the National Health Insurance (NHI) for Elderly Care in South Korea. Healthcare (Basel, Switzerland), 10(5), 779. https://doi.org/10.3390/healthcare10050779
Stuart, E. A., Huskamp, H. A., Duckworth, K., Simmons, J., Song, Z., Chernew, M., & Barry, C. L. (2014). Using propensity scores in difference-in-differences models to estimate the effects of a policy change. Health services & outcomes research methodology, 14(4), 166–182. https://doi.org/10.1007/s10742-014-0123-z
Werner, R. M., Konetzka, R. T., & Polsky, D. (2013). The effect of pay-for-performance in nursing homes: evidence from state Medicaid programs. Health services research, 48(4), 1393–1414. https://doi.org/10.1111/1475-6773.12035
Suggested Citation
Saluja, S. and Cartagena-Farias, J. (2024) Difference-in-Differences approach. GOLTC Methods Guide series, 1. Global Observatory of Long-Term Care, Care Policy & Evaluation Centre, London School of Economics and Political Science. https://goltc.org/publications/difference-in-differences-approach

