Authors & affiliations
Joaquín Mayorga1 and Javiera Cartagena-Farias2
1 Department of Social Policy and Care Policy and Evaluation Centre (CPEC), London School of Economics and Political Science
2 Care Policy and Evaluation Centre (CPEC), London School of Economics and Political Science
Introduction
Propensity Score Matching (PSM) is a quasi-experimental method used to create a control group by matching “treated” units (i.e., those participating in a programme or intervention) with non-treated units of similar observable characteristics before the intervention took place (Rosenbaum & Rubin, 1983). Unlike randomised controlled trials, PSM is employed in observational studies where randomisation is not feasible. Its main aim is to perform an impact evaluation. The premise is that the treated and the comparison group should have had similar characteristics before the intervention took place, and therefore had a similar likelihood to be (self or not self) selected for participation in the intervention to be evaluated. Thus, it is fair to compare these two groups after the treatment takes place.
In this regard, PSM aims to reduce selection bias by matching treated and untreated units of analysis with similar propensity scores. A propensity score represents the probability of a unit receiving treatment, given a set of observed characteristics (i.e., covariates). By matching treated and untreated units with similar propensity scores, PSM creates a sample in which the distribution of covariates is similar (balanced) between the treated and control groups. Intuitively, PSM constructs a statistical ‘clone’ in the control group as a counterfactual for each unit in the treatment group, determining how they would have performed if they had not received the intervention (Caliendo & Kopeinig, 2008).
The fundamental assumption behind PSM is the Conditional Independence Assumption (CIA), which states that, after adjusting for a relevant set of observable variables, the potential outcomes for both the treated and untreated groups would be identical in the absence of the intervention (Imbens, 2001). Therefore, differences in outcomes can be attributed to the intervention under study.
Description
To undertake a PSM approach to assess the effect of an intervention, it is necessary to have a well-defined treatment group (D=1) and control group (D=0), and a comprehensive set of observed covariates (X) that influence the likelihood of receiving the treatment at baseline (to estimate the propensity score of participation for each treated and untreated unit of analysis). Information on outcomes (Y) for both groups post-treatment is also required to assess the impact of the intervention accurately (information on pre-treatment is, however, not needed). In addition, having an adequate sample size is essential to ensure that there are enough treated and control units to achieve sufficient matches based on propensity scores.
The implementation of the PSM consist of the following steps:
1. Estimation of propensity scores: Employ a probit or logistic regression model to estimate the probability of receiving treatment based on the observed covariates.
![]()
2. Predict the probability of participation for each unit and restrict the sample to the common support: Restricting the sample to units that fall within the range of propensity scores overlapping between the treatment and control groups ensures that only comparable units from both groups are included in the analysis (see figure below).
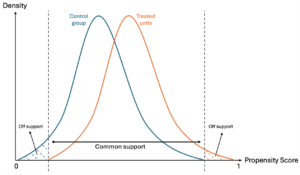
3. Match treated and control units based on the predicted propensity scores: Common matching methods include nearest-neighbor matching, caliper matching, and kernel matching, with the choice depending on factors such as the sample size, the number of treated and control observations available, and the distribution of the estimated propensity scores (Caliendo & Kopeinig, 2008).
4. Assess the balance of covariates between the treated and matched control groups: This can be achieved using standardised mean differences or other balance diagnostic tests.
5. Estimate the treatment effect: Compare the outcomes of the matched treated and control units to estimate the Average Treatment Effect on the Treated (ATT).
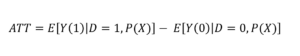
Where Y (1) is the outcome for the treated units and Y (0) is the outcome for the matched control units.
Limitations
It is worth noting that one potential complication may arise from the potential failure of the core Conditional Independence Assumption (CIA). Even if individuals are similar in terms of their observable characteristics, there may be significant unobservable factors that influence why some receive the treatment and others do not, which would introduce bias into the matching process and affect the reliability of the results. The main identifying assumption of PSM is argumentative rather than testable, meaning the methodology needs to be evaluated on a case-by-case basis, considering the specific context and characteristics of the study. Therefore, ensuring thorough documentation of the matching process and transparently discussing any limitations or potential sources of bias are important steps in reinforcing the credibility of the findings. Additionally, using longitudinal data to ensure the match is based on pre-treatment characteristics and conducting sensitivity analyses can further enhance the reliability of the results.
Example (in long-term care)
PSM is a widely used technique across various disciplines, including economics, social sciences, and public health. Some applications of the PSM approach to long-term care issues include the following:
- Schmitz & Westphal (2017) estimate the long-term effects of providing informal care on female caregivers’ labour market outcomes in Germany.
- Stöckel & Bom (2022) employ PSM to estimate the long-term and dynamic effects of providing informal care on the health of caregivers in the UK.
- Cartagena-Farias & Brimblecombe (2023) assess the total costs to the State associated with providing unpaid care in the UK.
- Kawabata & Fukuda (2023) look at the effects of a financial incentive scheme for dementia care on medical and long-term care expenditures.
Discussion
The original PSM technique, while widely used, has been subject to scrutiny and debate with regards to its ability to reduce selection bias. See for example:
- Guo S, Fraser M, Chen Q (2020) suggest that researchers need comprehensive knowledge of model assumptions and knowledge of plausible causal structure.
- Reiffel, J. (2020) applies the limitations and caveats of using PSM to the health and care context.
References
Caliendo, M. and Kopeinig, S. (2008). Some practical guidance for the implementation of propensity score matching. Journal of Economic Surveys.. 22, 1, 31–72.
Cartagena-Farias, J., & Brimblecombe, N. (2023). The economic cost of unpaid care to the public finances: inequalities in welfare benefits, forgone earnings-related tax revenue, and health service utilisation. Social Policy and Society. 1-15. https://doi.org/10.1017/S1474746423000477
Guo S, Fraser M, Chen Q (2020) Propensity score analysis: recent debate and discussion. J Soc Social Work Res. 11:463–482
Imbens, G. (2000). The role of the propensity score in estimating dose–response functions. Biometrika. 87(3): 706–710
Kawabata J, and Fukuda H (2023) Effects of a financial incentive scheme for dementia care on medical and long-term care expenditures: A propensity score–matched analysis using LIFE study data. PLoS ONE. 18(3): e0282965. https://doi.org/10.1371/journal.pone.0282965
Reiffel, J. (2020) Propensity Score Matching: The ‘Devil is in the Details’ Where More May Be Hidden than You Know. The American Journal of Medicine. 133 (2). https://doi.org/10.1016/j.amjmed.2019.08.055.
Rosenbaum, P. R. and Rubin, D. B. (1983), “The central role of the propensity score in observational studies for causal effects”. Biometrika, 70, 1, 41–55.
Rubin, D. B. (2001). Using propensity scores to help design observational studies: application to the tobacco litigation. Health Services Outcomes Research Methodology. 2, 3, 169–188.
Schmitz, H., & Westphal, M. (2017). Informal care and long-term labor market outcomes. Journal of Health Economics. 56, 1-18.
Stöckel, J., & Bom, J. (2022). Revisiting longer-term health effects of informal caregiving: Evidence from the UK. The Journal of the Economics of Ageing. 21, 100343.
Stuart, E. A., Huskamp, H. A., Duckworth, K., Simmons, J., Song, Z., Chernew, M., & Barry, C. L. (2014). Using propensity scores in difference-in-differences models to estimate the effects of a policy change. Health services & outcomes research methodology. 14(4), 166–182. https://doi.org/10.1007/s10742-014-0123-z
Suggested Citation
Mayorga, J. and Cartagena-Farias, J. (2024) Propensity Score Matching (PSM) methods. GOLTC Methods Guide series, 4. Global Observatory of Long-Term Care, Care Policy and Evaluation Centre, London School of Economics and Political Science. https://goltc.org/publications/propensity-score-matching-psm-methods/

